(Paper) AISTATS 2023 - Origins of Low-Dimensional Adversarial Perturbations
I am thrilled to announced that my paper called Origins of Low-Dimensional Adversarial Perturbations with Elvis Dohmatob and Chuan Guo from Meta AI Research has been accepted and will be published at AISTATS 2023! It has been selected to be one of the 32 papers to have an “oral” presentation :) Go check it for more details.
Here I will just detail a bit a concept that is important in our paper, which is called “Adversarially Viable Subspaces”. Let’s get to it.
General moivation and summary for a broad audience
It has been shown a few years ago that neural networks, even though very efficient to solve classification tasks with incredible accuracy, are vulnerable to malevolent perturbations of the input data that are imperceptible to humans.
The existence of these “adversarial examples” means that our models can fail critically when facing some data. The analysis of adversarial examples (do they always exists, when do they occur, why do they fool neural networks?) is currently an important research area for obvious security reasons (think about an autonomous car that ignores a stop sign).
Recently, some experimental works have shown that it is possible to craft adversarial examples by modifying a random low-dimensional subspace of the data. In other word, this means that we can create adversarial examples by randomly changing solely some pixels of an image. This makes the crafting of adversarial examples both practical (it is not difficult to generate random perturbations, knowing the model is not necessary) and efficient (you just have to change a small amount of the data), which raises a major issue.
We tackled this problem by studying the theory behind these experimental works to find what would be the smallest theoretical percentage of the data that could be attacked in such a context.
Focus on Adversarially Viable Subspaces
Let’s focus on a concept that we critically rely onto in our paper: Adversarially Viable Subspace. I will dig more into the maths to provide nice intuitions and explanations about it.
Settings
Binary classifier
We will conduct our analysis on binary classification tasks, where $X=(X_1,…,X_d) \in \mathbb{R}^d$ denotes an input of dimension $d$ (e.g. for the classical MNIST dataset, $d=784$) drawn from a probability distribution $\mathbb{P}_X$ on $\mathbb{R}^d$. We will denote by $f : \mathbb{R}^d \to \mathbb{R}$ the feature map, and $h_f = \text{sign} \circ f$ the corresponding classifier.
Importantly, since we are dealing with binary classification, we can identify the classifier $h_f$ with the negative decision region $C=${$x \in \mathbb{R}^d \mid h_f(x) = -1$} $= ${$x \in \mathbb{R}^d \mid f(x) \le 0$}
Now, given an input $x \in C’$ classified by $h_f$ as positive, an adversarial perturbation for $x$ is a vector $\Delta x \in \mathbb{R}^d$ of size $|\Delta x|$ such that $x + \Delta x \in C$. The goal of the attacker is to move points from $C’$ to $C$ with small perturbations.
Low-Dimensional Adversarial Perturbations
The adversarial perturbations $\Delta x$ are limited to a $k$-dimensional subspace $V$ of $\mathbb R^d$ whose choice is left to the attacker, but that should be of dimension $k$ smaller than $d$.
Given a subspace $V$ of $\mathbb R^d$, let $C^\varepsilon_V$ be the set of all points in $\mathbb R^d$ which can be pushed into the negative decision-region $C$ by adding a perturbation of size $\varepsilon$ in $V$, that is $C^\varepsilon_V := {x \in \mathbb{R}^d \mid \exists v \in V\text{ with }|v| \le \varepsilon \text{ s.t } x + v \in C }$
Finally, given an attack budget $\varepsilon \ge 0$, the fooling rate $\text{FR}(V;\varepsilon)$ of a subspace $V \subseteq \mathbb R^d$ is the proportion of test data which can be moved from the positive decision-region $C’$ to the negative decision-region $C$ by moving a distance $\varepsilon$ along $V$, that is $\text{FR}(V;\varepsilon) := \mathbb{P}_X(X \in C^\varepsilon_V \mid X \in C’)$.
Adversarially Viable Subspace
Definition
Since we work with low-dimensional perturbations that belongs to a subspace $V$ of small dimension, it possible that whatever the budget $\varepsilon$ given, even if it is very high, no perturbations will transport an input $x \in C’$ from the negative decision region to the positive one when adding perturbation $v$. In other word, it is possible that for a fixed $x \in C’$, $\forall \varepsilon > 0, x \not \in C^\varepsilon_V$.
This is the reson why we need to define which type of adversarial subspaces are sensible, which we call adversarially viable subspace. Formally, it is defined as:
[Definition:Adversarially viable subspace] Given $\alpha \in (0,1]$ and $\delta \in [0,1)$, a random subspace $V \subseteq \mathbb R^d$ is said to be adversarially $(\alpha,\delta)$-viable (w.r.t $C’$) if \begin{align} \mathbb{P}_{X,V}(|\Pi_V \eta(X)| \ge \alpha \mid X \in C’) \ge 1-\delta, \end{align}
where $\eta(x):=\nabla f(x)/|\nabla f(x)|$ is the gradient direction at $x$.
Let’s illustrate this notion with the following drawing:
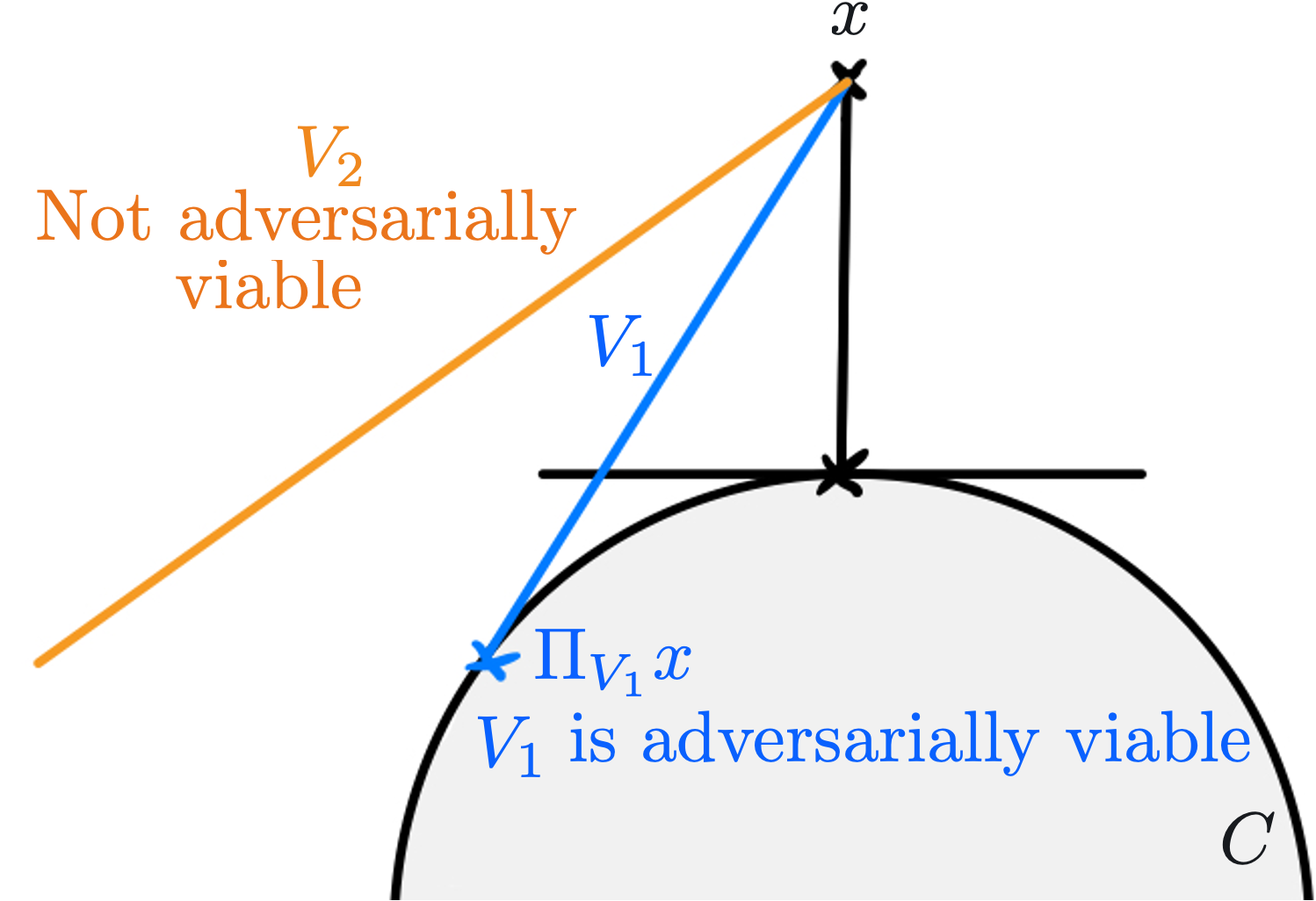
Intuition using a small example
Let’s consider the following simple case: the classifier is linear, and so $\forall x, \; f(x)= x^T w + b$. The negative decision region is then the simple half-space defined by: $C’=${$x \in \mathbb{R}^d \mid x^T w + b \leq 0$}
In that case, let’s study the fooling rate:
\[\begin{aligned} \text{FR}(V;\varepsilon) &:= \mathbb{P}_X (X \in C^\varepsilon_V \mid X \in C') \\ & \geq \sup_{v \in V} \mathbb{P}_X (X \in C_v^\varepsilon \mid X \in C')\\ & = \sup_{v \in V \cap \mathcal{S}_{d-1}} \mathbb{P}_X(X^T w + \varepsilon v^T w + b \leq 0 \mid X \in C')\\ & = \mathbb{P}_X(X^T w + b \le \varepsilon || \Pi_V w || \mid X \in C') \end{aligned}\]We manage to obtain a lower-bound, but we are stuck with the term $| \Pi_V w |$, which we can’t evaluate since $V$ is random. In that simple linear case, we can use concentration inequalities to obtain the following:
\[\|\Pi_V w\| \ge \sqrt{k/d}-t \text{ w.p.} 1-2e^{-t^2d/2}\]Notice the similarity between this inequality and the definition of the adversarially viable subspace. In essence, the notion of adversarially viable subspace allows us to generalize this kind of argument to more genral cases.